What Effect Does The Sample Size Have On The Standard Deviation Of All Possible Sample Means?
The Central Limit Theorem
34 The Central Limit Theorem for Sample Means
The sampling distribution is a theoretical distribution. It is created by taking many many samples of size n from a population. Each sample mean is then treated like a single ascertainment of this new distribution, the sampling distribution. The genius of thinking this way is that it recognizes that when we sample nosotros are creating an ascertainment and that observation must come from some particular distribution. The Fundamental Limit Theorem answers the question: from what distribution did a sample mean come? If this is discovered, and so we tin can treat a sample hateful just similar any other observation and summate probabilities about what values it might accept on. We have effectively moved from the world of statistics where we know merely what nosotros have from the sample, to the world of probability where we know the distribution from which the sample mean came and the parameters of that distribution.
The reasons that 1 samples a population are obvious. The time and expense of checking every invoice to determine its validity or every shipment to see if it contains all the items may well exceed the cost of errors in billing or shipping. For some products, sampling would require destroying them, chosen destructive sampling. 1 such instance is measuring the ability of a metal to withstand saltwater corrosion for parts on sea going vessels.
Sampling thus raises an of import question; simply which sample was drawn. Fifty-fifty if the sample were randomly drawn, there are theoretically an almost infinite number of samples. With just 100 items, at that place are more than than 75 million unique samples of size five that can be fatigued. If 6 are in the sample, the number of possible samples increases to just more one billion. Of the 75 one thousand thousand possible samples, so, which one did yous go? If there is variation in the items to exist sampled, in that location volition be variation in the samples. One could draw an "unlucky" sample and make very wrong conclusions concerning the population. This recognition that any sample we draw is really merely i from a distribution of samples provides us with what is probably the single most important theorem is statistics: the Central Limit Theorem. Without the Key Limit Theorem it would exist impossible to proceed to inferential statistics from simple probability theory. In its most bones grade, the Central Limit Theorem states that regardless of the underlying probability density office of the population information, the theoretical distribution of the means of samples from the population will exist normally distributed. In essence, this says that the hateful of a sample should be treated like an observation fatigued from a normal distribution. The Cardinal Limit Theorem but holds if the sample size is "large enough" which has been shown to exist just 30 observations or more.
(Effigy) graphically displays this very of import proposition.
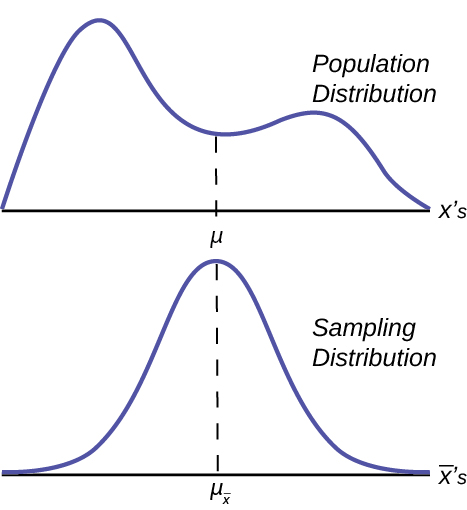
Detect that the horizontal axis in the top panel is labeled X. These are the individual observations of the population. This is the unknown distribution of the population values. The graph is purposefully fatigued all squiggly to bear witness that it does not matter just how odd ball it actually is. Call up, nosotros volition never know what this distribution looks similar, or its mean or standard deviation for that matter.
The horizontal centrality in the bottom panel is labeled ![]() 's. This is the theoretical distribution called the sampling distribution of the means. Each observation on this distribution is a sample hateful. All these sample means were calculated from private samples with the aforementioned sample size. The theoretical sampling distribution contains all of the sample mean values from all the possible samples that could have been taken from the population. Of course, no i would ever actually take all of these samples, simply if they did this is how they would look. And the Central Limit Theorem says that they will be normally distributed.
's. This is the theoretical distribution called the sampling distribution of the means. Each observation on this distribution is a sample hateful. All these sample means were calculated from private samples with the aforementioned sample size. The theoretical sampling distribution contains all of the sample mean values from all the possible samples that could have been taken from the population. Of course, no i would ever actually take all of these samples, simply if they did this is how they would look. And the Central Limit Theorem says that they will be normally distributed.
The Fundamental Limit Theorem goes even further and tells us the mean and standard difference of this theoretical distribution.
| Parameter | Population distribution | Sample | Sampling distribution of |
|---|---|---|---|
| Mean | μ | | |
| Standard deviation | σ | s | |
The practical significance of The Central Limit Theorem is that at present we can compute probabilities for drawing a sample hateful, ![]() , in merely the same way every bit we did for drawing specific observations, Ten'southward, when we knew the population mean and standard departure and that the population data were normally distributed.. The standardizing formula has to be amended to recognize that the mean and standard departure of the sampling distribution, sometimes, called the standard error of the hateful, are different from those of the population distribution, but otherwise nothing has changed. The new standardizing formula is
, in merely the same way every bit we did for drawing specific observations, Ten'southward, when we knew the population mean and standard departure and that the population data were normally distributed.. The standardizing formula has to be amended to recognize that the mean and standard departure of the sampling distribution, sometimes, called the standard error of the hateful, are different from those of the population distribution, but otherwise nothing has changed. The new standardizing formula is
![]()
Notice that ![]() in the first formula has been changed to simply µ in the second version. The reason is that mathematically it can be shown that the expected value of
in the first formula has been changed to simply µ in the second version. The reason is that mathematically it can be shown that the expected value of ![]() is equal to µ. This was stated in (Figure) to a higher place. Mathematically, the E(10) symbol read the "expected value of ten". This formula will be used in the adjacent unit of measurement to provide estimates of the unknown population parameter μ.
is equal to µ. This was stated in (Figure) to a higher place. Mathematically, the E(10) symbol read the "expected value of ten". This formula will be used in the adjacent unit of measurement to provide estimates of the unknown population parameter μ.
Chapter Review
In a population whose distribution may be known or unknown, if the size (due north) of samples is sufficiently large, the distribution of the sample means will be approximately normal. The mean of the sample means will equal the population mean. The standard departure of the distribution of the sample ways, called the standard fault of the mean, is equal to the population standard deviation divided by the square root of the sample size (n).
Formula Review
The Key Limit Theorem for Sample Means:
![]() ~ N
~ N ![]()
![]()
The Mean ![]()
Central Limit Theorem for Sample Means z-score ![]()
Standard Error of the Mean (Standard Deviation (![]() )):
)): ![]()
Finite Population Correction Factor for the sampling distribution of ways: ![]()
Finite Population Correction Factor for the sampling distribution of proportions: ![]()
Homework
Previously, De Anza statistics students estimated that the amount of modify daytime statistics students carry is exponentially distributed with a mean of ?0.88. Suppose that nosotros randomly pick 25 daytime statistics students.
- In words, Χ = ____________
- Χ ~ _____(_____,_____)
- In words,
 = ____________
= ____________ -
 ~ ______ (______, ______)
~ ______ (______, ______) - Detect the probability that an private had between ?0.eighty and ?1.00. Graph the state of affairs, and shade in the area to be determined.
- Find the probability that the average of the 25 students was between ?0.fourscore and ?one.00. Graph the situation, and shade in the area to be determined.
- Explain why there is a difference in part e and part f.
<!– <solution id="id6274098″> Due north ( 250, fifty 49 ) 0.0808 256.01 anxiety –>
According to the Internal Revenue Service, the average length of time for an individual to complete (keep records for, learn, prepare, copy, assemble, and send) IRS Form 1040 is 10.53 hours (without any fastened schedules). The distribution is unknown. Let us presume that the standard deviation is ii hours. Suppose we randomly sample 36 taxpayers.
- In words, Χ = _____________
- In words,
 = _____________
= _____________ -
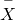 ~ _____(_____,_____)
~ _____(_____,_____) - Would y'all exist surprised if the 36 taxpayers finished their Course 1040s in an average of more than 12 hours? Explain why or why not in consummate sentences.
- Would yous be surprised if i taxpayer finished his or her Form 1040 in more than 12 hours? In a consummate sentence, explicate why.
- length of time for an individual to complete IRS form 1040, in hours.
- mean length of time for a sample of 36 taxpayers to consummate IRS form 1040, in hours.
- N
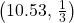
- Yes. I would be surprised, because the probability is most 0.
- No. I would not be totally surprised because the probability is 0.2312
Suppose that a category of earth-grade runners are known to run a marathon (26 miles) in an average of 145 minutes with a standard deviation of 14 minutes. Consider 49 of the races. Let ![]() the average of the 49 races.
the average of the 49 races.
-
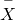 ~ _____(_____,_____)
~ _____(_____,_____) - Find the probability that the runner will boilerplate between 142 and 146 minutes in these 49 marathons.
- Find the 80th percentile for the boilerplate of these 49 marathons.
- Find the median of the boilerplate running times.
<!– <solution id="id6533816″> N ( 145, 14 49 ) 0.6247 146.68 145 minutes –>
The length of songs in a collector's iTunes album collection is uniformly distributed from two to 3.5 minutes. Suppose we randomly pick five albums from the collection. There are a total of 43 songs on the v albums.
- In words, Χ = _________
- Χ ~ _____________
- In words,
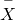 = _____________
= _____________ -
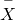 ~ _____(_____,_____)
~ _____(_____,_____) - Find the first quartile for the boilerplate song length.
- The IQR(interquartile range) for the average song length is from _______–_______.
- the length of a song, in minutes, in the collection
- U(two, 3.five)
- the average length, in minutes, of the songs from a sample of five albums from the collection
- Northward(two.75, 0.066)
- 2.74 minutes
- 0.03 minutes
<!– <solution id="fs-idm55467904″> the size of a U.S. farm in 1940 the average size of a U.Southward. farm, in acres Northward ( 174, 55 38 ) 168.0, 180.0 –>
- True. The mean of a sampling distribution of the means is approximately the mean of the information distribution.
- Truthful. Co-ordinate to the Cardinal Limit Theorem, the larger the sample, the closer the sampling distribution of the ways becomes normal.
- The standard difference of the sampling distribution of the means will decrease making it approximately the same every bit the standard deviation of X as the sample size increases.
The percent of fatty calories that a person in America consumes each day is usually distributed with a mean of about 36 and a standard deviation of about ten. Suppose that 16 individuals are randomly chosen. Let ![]() = average percent of fat calories.
= average percent of fat calories.
-
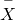 ~ ______(______, ______)
~ ______(______, ______) - For the group of 16, find the probability that the average percent of fat calories consumed is more than v. Graph the situation and shade in the expanse to exist determined.
- Find the first quartile for the average percentage of fatty calories.
<!– <solution id="id6272525″> N ( 36, 10 16 ) one 34.31 –>
The distribution of income in some Third Globe countries is considered wedge shaped (many very poor people, very few middle income people, and even fewer wealthy people). Suppose we pick a state with a wedge shaped distribution. Let the average bacon exist ?ii,000 per year with a standard deviation of ?8,000. Nosotros randomly survey ane,000 residents of that country.
- In words, Χ = _____________
- In words,
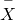 = _____________
= _____________ -
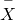 ~ _____(_____,_____)
~ _____(_____,_____) - How is information technology possible for the standard deviation to be greater than the average?
- Why is it more likely that the boilerplate of the one,000 residents volition be from ?2,000 to ?2,100 than from ?2,100 to ?ii,200?
Which of the following is NOT True about the distribution for averages?
- The mean, median, and mode are equal.
- The area nether the curve is i.
- The curve never touches the x-axis.
- The curve is skewed to the correct.
<!– <solution id="id6538477″> d –>
Key Terms
- Average
- a number that describes the central tendency of the information; there are a number of specialized averages, including the arithmetic mean, weighted mean, median, mode, and geometric mean.
- Primal Limit Theorem
- Given a random variable with known hateful μ and known standard deviation, σ, we are sampling with size n, and we are interested in two new RVs: the sample mean,
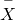 . If the size (north) of the sample is sufficiently large, then
. If the size (north) of the sample is sufficiently large, then 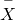 ~ Due north(μ,
~ Due north(μ, 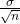 ). If the size (north) of the sample is sufficiently large, then the distribution of the sample ways volition estimate a normal distributions regardless of the shape of the population. The mean of the sample ways will equal the population mean. The standard difference of the distribution of the sample ways,
). If the size (north) of the sample is sufficiently large, then the distribution of the sample ways volition estimate a normal distributions regardless of the shape of the population. The mean of the sample ways will equal the population mean. The standard difference of the distribution of the sample ways, 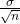 , is chosen the standard error of the mean.
, is chosen the standard error of the mean.
- Standard Error of the Mean
- the standard deviation of the distribution of the sample means, or
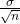 .
.
What Effect Does The Sample Size Have On The Standard Deviation Of All Possible Sample Means?,
Source: https://opentextbc.ca/introbusinessstatopenstax/chapter/the-central-limit-theorem-for-sample-means/
Posted by: farrararkmadesain.blogspot.com


0 Response to "What Effect Does The Sample Size Have On The Standard Deviation Of All Possible Sample Means?"
Post a Comment